#221 最大正方形(动态规划)

221. 最大正方形 - 力扣（LeetCode）

状态描述：dp[i][j]表示，(i,j)作为正方形右下角，其正方形最大边长。

一个边长为a的正方形，(i-1,j)，(i,j-1)，(i-1,j-1)都应该满足是至少是最大边长为a-1的正方形右下角。

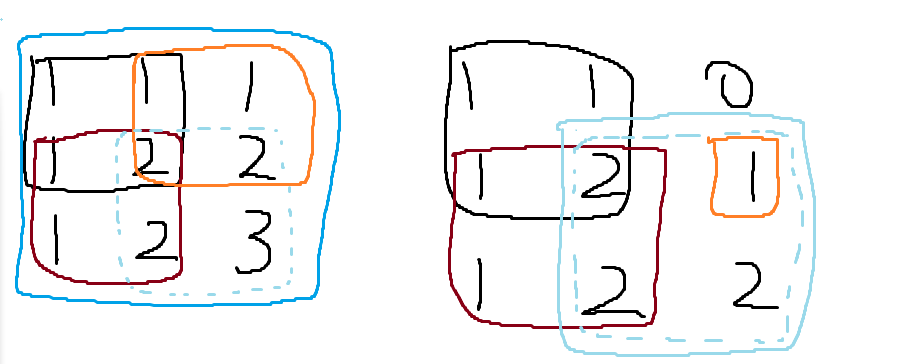状态转移方程：dp[i][j]=0/(1+min(dp[i-1][j],dp[i][j-1],dp[i-1][j-1]))

class Solution {
public:
    int maximalSquare(vector<vector<char>>& matrix) {
        int m=matrix.size();
        int n=matrix[0].size();
        vector<vector<int>> dp(m,vector<int>(n,0));
        dp[0][0]=(matrix[0][0]=='1');
        int max=0;
        for(int i=0;i<m;i++)
            for(int j=0;j<n;j++){
                if(matrix[i][j]=='0') dp[i][j]=0;
                else{
                    if(j-1<0 || i-1 <0) dp[i][j]=1;
                    else{
                        int left=dp[i][j-1];
                        int up=dp[i-1][j];
                        int corn=dp[i-1][j-1];
                        int min=left;
                        if(up<min) min=up;
                        if(corn<min) min=corn;
                        dp[i][j]=min+1;
                    }
                    if(dp[i][j]>max) max=dp[i][j];
                }
                
            }
        return max*max;
    }
};