#5 最长回文子串(动态规划)

5. 最长回文子串 - 力扣（LeetCode）

class Solution {
public:
    bool isrvs(string s) {
        for (int i = 0; i < s.size() / 2; i++)
            if (s[i] != s[s.size() - 1 - i]) return false;
        return true;
    }
    string longestPalindrome(string s) {
        if (!s.size() || s.size() == 1) return s;
        string result = s.substr(0,1);
        for (int i = 0; i < s.size()-1; i++) {
            for (int lenth = 2; i + lenth <= s.size(); lenth++) {
                string sub = s.substr(i, lenth);
                if (isrvs(sub) && sub.size() > result.size()) result = sub;
            }
        }
        return result;
    }
};

超时。原因在于每次都重新判断，无法利用回文中两面包夹芝士的特性，产生递推式。

提示：状态dp[i][j]为s.substr(i,j-i+1)是否为回文串

状态描述：dp[i][j]为s.substr(i,j-i+1)是否为回文串。该二维向量左对角线以右都是无效状态(非法字符串)。

状态转移方程：dp[i][j]=(s[i]!=s[j]) && dp[i+1][j-1](包裹串)

判断如cbba这种，中间只有两个字符的回文串。dp[1][2]不能使用原方程，当作初态生成。

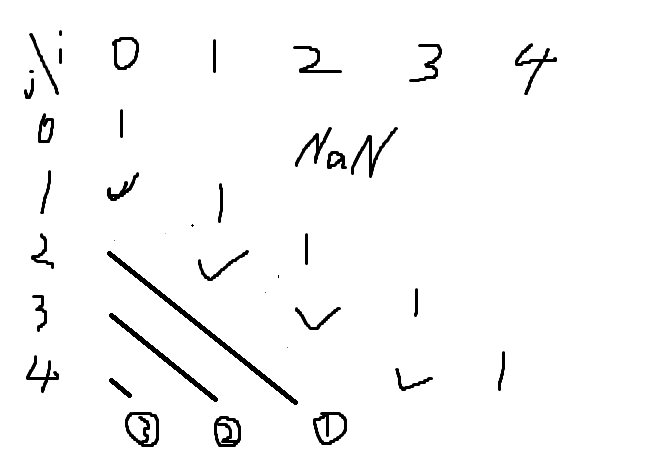
如图，状态转移依赖右上角dp。

初态：dp[i][i]=1 dp[i][i+1]=0/1 初始化对角线及相邻一列平行线。

class Solution {
public:
    string longestPalindrome(string s) {
        if(s.size()<=1) return s;
        if(s.size()==2){
            if(s[0]==s[1]) return s;
            else return s.substr(0,1);
        }
        vector<vector<int>> dp(s.size(),vector<int>(s.size(),0));  
        //init dp
        for(int i=0;i<s.size();i++){
            dp[i][i]=1;
            if(i+1<s.size()&&s[i]==s[i+1])  dp[i][i+1]=1;
        }
        //update dp,dp[i][j]=0/dp[i+1][j-1]
        for(int step=2;step<s.size();step++)
            for(int i=0;i+step<s.size();i++)
                if(s[i]==s[i+step])
                    dp[i][i+step] = dp[i+1][i+step-1];
        
        string max;
        max="";
        bool found=0;
        //find max
        for(int step=s.size()-1;!found&&step>=0;step--)
            for(int i=0;!found&&i+step<s.size();i++)
                if(dp[i][i+step]){
                    max=s.substr(i,step+1);
                    found=1;
                }
        return max;
    }
};